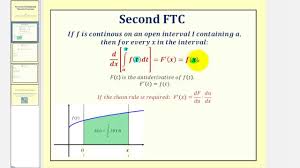
The second fundamental theorem of calculus states that:. The derivative of a definite integral with a variable upper limit is equal to the integrals function evaluated at that upper limit.
suppose that f is continuous between closed interval [a, b], if G is any anti-derivative of f on the closed interval [a, b], then:
$$\int_{a}^{b} = [G(x) +c]_{a}^{b} = [G(b) +c] – [G(a) +c]$$
$$ = G(b) + c – G(a) -c = G(b) – G(a)$$
if you have a function defined as the integral of another function (with a variable upper bound), taking the derivative of the integral function simply replaces the variable of integration in the original function with the upper limit.
Example problem on second fundamental theorem of calculus
Evaluate the following definite integrals:
$$ a) \ \int_{0}^{3} x^2 dx $$
$$ a) \ \int_{0}^{1} x^2 \sqrt{x^3+1} dx $$
solution
$$ a) \ \int_{0}^{3} x^2 dx =\left[ \frac{x^3}{3} + c \right]_{a}^{b} = \left[ \frac{3^3}{3} + c \right]-\left[ \frac{0^3}{3} + c \right]$$
$$= \frac{27}{3}-0 =9$$
$$ b) \ \int_{0}^{1} x^2 \sqrt{x^3+1} dx $$
$$ let \ u= x^3 +1 $$
$$\int_{0}^{1} = x^2 \sqrt{u} \frac{du}{3x^2} = \frac{1}{3} \int_{1}^{2} u^{\frac{1}{2}}du $$
$$du = 3x^2dx$$
$$dx = \frac{du}{3x^3} $$
$$\int_{0}^{1} x^2 \sqrt{u} \frac{du}{3x^2} = \frac{1}{3} \int_{1}^{2} u^{\frac{1}{2}} du$$
\[
= \frac{u^{\frac{3}{2}}}{\frac{3}{2}} + c = \frac{1}{3} \left[\frac{2u^{\frac{3}{2}}}{3}\right] + c
\]
$$= \frac{2u^{\frac{3}{2}}}{9} + c$$
$$ \left[ \frac{2x^3 + 1}{9} + c \right]_0^1 = \frac{2}{9}(2)^{\frac{3}{2}}+c -( \frac{2}{9}(1)^{\frac{3}{2}}+c)$$
$$=\frac{2}{9}\left[2^{\frac{3}{2}}-1 \right] + c $$
Example
$$\int_{2}^{3}x \sqrt{x-2}dx $$
$$ let u = x-2 $$
$$ x = u+2$$
$$\int_{2}^{3}(u+2) \sqrt{u} du = \int (u+2) ^{\frac{1}{2}} du = \int u^{\frac{3}{2}} + 2u^{\frac{3}{2}}du$$
$$=\frac{2u^{\frac{5}{2}}}{5} +\frac{ 4u^{\frac{3}{2}}}{3}+ c$$
$$=\left[\frac{2(x-2)^{\frac{5}{2}}}{5} +\frac{ 4(x-2)^{\frac{3}{2}}}{3}+ c \right]_2^3$$
replacing x for 2 and 3;
$$=\left[\frac{2(3-2)^{\frac{5}{2}}}{5} +\frac{ 4(3-2)^{\frac{3}{2}}}{3}+ c \right]_2^3 -\left[\frac{2(2-2)^{\frac{5}{2}}}{5} +\frac{ 4(2-2)^{\frac{3}{2}}}{3}+ c \right]_2^3 $$
$$=\left[\frac{2(1)^{\frac{5}{2}}}{5} +\frac{ 4(1)^{\frac{3}{2}}}{3}+ c \right]_2^3 -\left[\frac{2(0)^{\frac{5}{2}}}{5} +\frac{ 4(0)^{\frac{3}{2}}}{3}+ c \right]_2^3 $$
$$\frac{2}{5} + \frac{4}{3} = \frac{26}{15} $$
Example
$$(d) \ \int_{0}^{\frac{\pi}{2}} xcosxdx $$
solution
from integration by parts:
$$udv = uv – \int vdu$$
$$let \ u = x$$
$$dv = cos x$$
$$v=sin x$$
$$du=1 dx$$
$$(d) \ \int_{0}^{\frac{\pi}{2}} xcosxdx = xinx – \int sinxdx$$
$$ \left [xsinx – cosx+c \right]_{0}^{\frac{\pi}{2}}= \frac{\pi}{2}sin\frac{\pi}{2} – cos\frac{\pi}{2}=\frac{pi}{2}$$
Example
$$e) Evaluate: \ \int \frac{x+2}{x^2-5x+6}$$
solution
$$\int \frac{x+2}{x^2-5x+6}=\frac{x+2}{(x-2)(x-3)}dx=\frac{A}{x-2} + \frac{B}{x-3}$$
comparing denominator and the numerator:
$$A(x-3)+B(x-2) = x +2$$
$$Ax-3A+Bx-2B = x +2 $$
$$Ax+bx=x$$
$$-3A-2B=2$$
$$A +B=1$$
$$-3A-2B=2$$
solving the two equations above simultaneously;
B=5 and A=-4
Rewriting the integral equation:
$$\int \frac{x+2}{x^2-5x+6}dx = -4 \int_{1}^{2} \frac{1}{x-2} + 5\int_{1}^{2} \frac{1}{x-3}dx $$
$$\left [ -4ln|x-2| +5ln|x-3| \right ]_{1}^{2}$$
$$=\left [ -4ln 0 +5 ln1 \right] – [-ln1 + 5ln2]$$
$$\left [ \infty+0 \right] – \left [0 +5ln2 \right]$$
Example
$$\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} cos^3xdx$$
solution
Using trigonometric identities, the integral becomes:
$$\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} cos^3xdx =\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} cos^2xcosxdx = \int(1-sin^2x)cosxdx$$
$$\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} cosx – sin^2xcosxdx =\left[sinx – \frac{1}{3}sin^3x \right]_{\frac{-\pi}{2}}^{\frac{\pi}{2}}$$
$$\left [1-\frac{1}{3} – [-1 + \frac{1}{3} \right] = \frac{2}{3} +1 – \frac{1}{3} = \frac{4}{3} $$
Revision exercise for second fundamental theorem of calculus
$$1. \int_{0}^{\frac{1}{2}} \frac{x}{\sqrt{1-x^2} }dx $$
$$2. \int_{0}^{4} 2x\sqrt{1-x^2} dx $$
$$3. \int_{0}^{\frac{\pi}{4}}sec^2xdx $$
$$4. \int_{0}^{\frac{\pi}{2}}sinx\sqrt{cosx}dx $$
$$5. \int_{0}^{1} xe^x dx $$
$$6. \int_{1}^{2} x^3lnx dx $$
$$7. \int_{0}^{1} \frac{1}{(4-x^2)^\frac{3}{2}}dx $$
$$8. \int_{\frac{1}{2}}^{1} \frac{x-2}{(x+2)^3(x-6)^3}dx $$
Answers to revision exercise
$$1. \ \ 1-\frac{1}{2}\sqrt{3}$$
$$2. \ \ \frac{256}{15}$$
$$3. \ \ \frac{4}{3}$$
$$4. \ \ \frac{2}{3}$$
$$5. \ \ 1$$
$$6. \ \ 4ln2-\frac{15}{16}$$
$$7. \\ \frac{\sqrt{3}}{12} \ or \ \frac{1}{4 \sqrt{3}}$$
$$8. \\ \frac{23}{10890}$$
Related topics

Comments
One response to “The second fundamental theorem of calculus”
[…] The second fundamental theorem of calculus […]