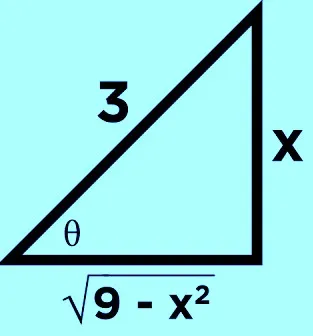Integration of trigonometric expressions -

Integrating trigonometric expressions involves solving trigonometric expressions that contain trigonometric functions. These functions are periodical. They denote the relationship between the angle and the sides of a right-angled triangle.

Examples of trigonometric functions includes:

sine
cosines
tangents
secants
cosecants
cotangents

There are various techniques used to integrate mathematical expressions with trigonometric functions. Integration of trigonometric expressions requires a mix of direct integration rules. This may includes simplification using identities, substitution, and sometimes integration by parts, depending on the form of the expression. some of the techniques includes:

Table of Contents

some know trigonometric functions and identities

some trigonometric identities are known to transform to another specific and definite trigonometric functions after the integration process. This can be very useful during Integrating trigonometric expressions. Some examples includes:

$$\int sinxdx = -cosx+c$$

The above expression shows that we always obtain a negative value of a cosine function. This negative value is accompanied by another constant number whenever the sine function is integrated.

$$\int cosxdx = sinx+c$$

in other words, integrating a cosine functions results to a positive value of a cosine function when Integrating trigonometric expressions.

(iii).∫sec²xdx=tanx+c

(iv).∫csc²xdx=−cotx+c

(v).∫secxtanxdx=−secx+c

(vi).∫cscxcotxdx=−cscx+c

2. Using trigonometric identities

by using trigonometric identities, some trigonometric expressions that could be complex to integrate becomes simplified .

When Integrating trigonometric expressions useful trigonometric identities includes:

$$sin^2x = \frac{1-cos2x}{2}$$

$$cos^2x = \frac{1+cos2x}{2}$$

$$sinxcosx = \frac{1}{2}sin2x$$

The above identities are known as power reduction identities

3. Substitution Method

Substitution method in integration is a used to simplify an integral by making a change of variables. This transforms the integral into a simpler form Integrating trigonometric expressions. It is often used when the integrand contains a composite function, making it easier to integrate.

Substitution generally has the following steps:

Identifying part of the integrand that can be replaced with a new variable (usually denoted by u).
Compute the derivative of the chosen substitution with respect to x (i.e., find du). This helps in expressing dx in terms of du.
Substitute u and du into the original integral, replacing the x-terms with the new u-terms. This aims at simplifying the integral so that it’s easier to solve.
Perform the integration with respect to u.
Once the integral is solved in terms of u, substitute the original expression for u back into the result to return to the variable x.

In trigonometric functions, the trigonometric ratio can have even or odd powers, which determines how they are treated during integration.

Integration of trigonometric expressions: 4. Integration by Parts

Integration by parts is a technique commonly used to integrate product of two functions. It is based on the product rule for differentiation derived from the following formula:

$$\int udv = uv – \int vdu $$

By applying the formula the above formula, you can reduce the complexity of the integral so that it is easier to solve.

Integration by parts may involves steps like:

Choose two functions from the integrand, u and dv, such that the integral of v is easier to compute than the original one
Compute du, the derivative of u.
Compute v, the integral of dv
Substitute u, dv, du, and v into the integration by parts formula.
If the resulting integral is easier to evaluate, solve it. If not, apply integration by parts again

Integration of trigonometric expressions: Trigonometric Substitution

This is used when the integrand involves square roots and trigonometric functions. consider the integral:

$$\int \frac{dx}{\sqrt{1-x^2}}$$

An integral that looks like the above expression can be solved first by substituting x for sinθ such that x -sinθ = 0.

that is: x= sinθ

Integrating Even powers of sine and cosine

Integrating even powers of sine and cosine involves simplifying the integral of expressions where the powers of sine n is an even integer. These integrals can often be simplified using power reduction identities.

When powers of a trigonometric ratios are even, the double angle identities becomes very useful. These identities reduce the even powers of sine and cosine to sums of trigonometric functions of lower powers. This process makes the integration easier. These identities includes:

$$cos^2\theta = \frac{1}{2}(1+cos2\theta)$$

$$sin^2\theta = \frac{1}{2}(1-cos2\theta)$$

Example problem on trigonometric substitution

$$cos^4d\theta = \int cos^2θcos^2θ = \int \frac{1}{2}(1+cos2θ) \frac{1}{2}(1+cos2θ)dθ$$

$$ \int \frac{1}{4}(1+cos2θ)^2dθ= \frac{1}{4}(1+cos2θ)(1+cos2θ)dθ$$

now we expand the binomial product to have:

$$ \int \frac{1}{4}(1+cos2θ)(1+cos2θ)dθ= \frac{1}{4}[1(1+cos2θ)+cos2θ(1+cos2θ)]dθ$$

$$=\frac{1}{4} \int (1+cos2θ+cos2θ+cos^22θ)dθ=\frac{1}{4} \int (1+2cos2θ+cos^22θ)dθ$$

$$cos^2 2θ = \frac{1}{4}(1+cos4θ)$$

Therefore:

$$=\frac{1}{4} \int (1+cos2θ+cos2θ+cos^22θ)dθ=\frac{1}{4} \int (1+2cos2θ+\frac{1}{4}(1+cos4θ)dθ$$

$$=\frac{1}{4}\int dθ+\frac{1}{2}\int cos2θ + \frac{1}{8}\int dθ+\frac{1}{8}\int cos4θdθ $$

$$=\frac{1}{4}\theta+\frac{1}{2}\frac{sin2\theta}{2}+\frac{1}{8}\theta+\frac{1}{8}\theta+\frac{1}{8}\frac{sin4\theta}{8} +c$$

simplifying we finally have:

$$=\frac{3θ}{8}+\frac{sin2θ}{4}+\frac{sin4θ}{32}+c$$

Example2

solve : ∫sin²4θdθ

solution

using double angle identities;

$$sin^24θ = \frac{1}{2}(1-cos8θ)dθ$$

remember the identity:

$$sin^2nθ = \frac{1}{2}(1-sin2nθ)$$

hence

$$sin^24θ = \int \frac{1}{2}(1-cos8θ)dθ$$

$$=\frac{1}{2} \int dθ – \frac{1}{2} \int cos8θdθ$$

integrating we find :

$$\frac{1}{2}θ-\frac{1}{16}sin8θ+c = \frac{θ}{2} – \frac{sin8θ}{16}+c$$

Solving Integrating trigonometric expressions with odd powers

while integrating this kind of trigonometric expressions, we use trigonometric identity which states that:

cos²θ+sin²θ=1

consider the integral:

∫sin⁵θdθ

we split the operation sin⁵θ into sin⁴θ(sinθ).

thus:

but sin⁴θ = (1-cos²θ)² from the identity stated earlier.

Expanding:

(1−cos²θ)²=(1−2cos²θ+cos⁴θ)θdθ

it follows that:

∫sin⁴θsinθdθ=∫(1−cos²θ)²sinθdθ

=∫(1−2cos2θ−cos4θ)sinθdθ

=∫(sinθ–2sinθcos²θdθ+sinθcos⁴θ)dθ

=∫sinθdθ–2∫sinθcos²θdθ+∫sinθcos⁴θdθ

remember the identity:

$$sin\theta cos^n \theta d \theta = \frac{-1}{n+1}cos^{n+1} \theta +c $$

hence

$$\int sin θcos^4θdθ = \frac{-1}{5}cos^5θ+c$$

similarly:

$$\int sinθcos^2θdθ = \frac{-1}{3}cos^3θ+c$$

hence,

$$=\int sinθdθ – 2 \int sinθcos^2θdθ+sinθcos^4θdθ $$$$= -cosθ+\frac{2}{3}cos^3θ-\frac{1}{5}cos^5θ+c$$

In general, integrating even power of sine and cosine constitutes the following procedure:

If the integrand contains an even power of sine or cosine, use the corresponding power reduction identity. This will simplify the expression.
After applying the identity, the integral often becomes easier to solve. This is because the powers of sine or cosine are reduced to terms involving cos⁡(2x) or constants. These terms can be integrated straightforwardly.
Repeat where necessary: If higher powers of sine or cosine appear, you may need to apply the power reduction identity. You might have to do this multiple times.

Example 3

solve: ∫cos³θdθ

solution

$$cos^3θ = cos^2θcosθ = (1-sin^2θ)cosθdθ =(cosθ-sin^2θ)$$

hence:

$$cos^3θ dθ= cos^2θcosθdθ $$ $$= (1-sin^2θ)cosθdθ =(cosθ-sin^2θcosθ)dθ$$

$$=(cosθ-sin^θcosθ)dθ = \int cosθdθ-\int sin^2θcosθdθ$$

and

$$ \int cosθdθ-\int sin^2θcosθdθ =sinθ-\frac{1}{3}sin^3θ+c$$

Example 4

solve:

∫tan³θdθ

solution

incase of tanθ, we use the identity :

1+tan²θ=sec2θ

∫tan³θdθ=∫tan²θtanθdθ=∫(sec²θ−1)tanθdθ

∫(sec²θ−1)tanθdθ=∫(sec²θtanθ−tanθ)dθ

=∫sec²θtanθdθ−∫tanθdθ

we can use integration by substitution to solve

∫sec²θtanθdθ

let u = tanθ

$$\frac{du}{d\theta}=sec^2 \theta d \theta$$

hence du = sec²θdθ

$$dθ=\frac{du}{sec^2dθ}$$

$$\int tanθsec^2θ \frac{du}{sec^θ}=\int tanθdu =\int udu $$

and

$$\int udu = \frac{u^2}{2}+c =\frac{ tan^2θ}{2}+c$$

and

∫tanθdθ=ln|cosθ|+c

hence

$$\int sec^2θtanθdθ – \int tanθdθ = \frac{tan^2θ}{2}+ln|cosθ|+c$$

Example 4

Solve the integral ∫sec⁶2xdx

solution

∫sec⁶2xdx=∫sec⁴2xsec²xdx=∫(1+tan²x)²sec²2xdx ——(i)

$$\int sec^62xdx = \int sec^42xsec^2xdx $$$$= \int (1+tan^2x)^2sec^22xdx——–(i)$$

that is:

$$sec^22x = 1+tan^22x$$ $$sec^42x=(sec^22x)^2=(1+tan^2 2x)^2$$

Expanding the equation (i) above:

$$\int (sec^2 2x + 2tan^2 2xsec^2 2x + tan^4 2xsec^ 2x)dx$$

which results to:

$$\int sec^ 2xdx+2 \int tan^62xsec^2xdx+\int tan^4 2xsec^2 2x dx$$

consider the integral;

$$sec^2 2xdx$$

let u=2x then:

$$\frac{dx}{du}=\frac{1}{2}$$

$$dx = \frac{1}{2}du$$

Therefore: du=2dx

$$sec^2 2xdx = \frac{1}{2} \int sec^udx = \frac{1}{2}tan u+c$$ $$\frac{tan2x}{2}+c————(ii)$$

consider the expression:

$$2 \int tan^ 2x sec^ 2x dx$$

let u = tan2x

du = 2sec²2xdx

$$dx = \frac{du}{2sec^2 2x}$$

dx=du2sec22x

the expression therefore becomes:

$$2\int tan^2 2x sec^2 2x dx = 2 \int u^2 2x \frac{du}{2sec^2 2x}$$ $$\int u^2du=\frac{u^3}{3}+c = \frac{tan^3 2x}{3}+c ——–(iii)$$

Using the same method and procedure:

$$tan^4 2x sec^2 2x dx = \frac{tan^5 2x}{10}+c ——(iv)$$

combining the results of (ii), (iii) and (iv), the integral becomes;

$$\int sec^6 2x dx = \frac{tan2x}{2}+\frac{tan^3 2x}{3}+\frac{tan^5 2x}{10}+c$$

Integration of trigonometric expressions: Multiple angles identities

Multiple angle identities are trigonometric identities that express trigonometric functions of multiple angles (such as 2θ, 3θ, etc.) in terms of simpler functions of a single angle θ. These identities are helpful in simplifying expressions involving trigonometric functions of multiple angles.

Some common multiple angles includes:

sin(A+B) +sin(A-B) = 2sinAcosB
cos(A+B) + cos(A-B) = 2cosAcosB
cos(A-B)-cos(A+B) = 2sinAsinB

Example 6

work out: ∫sin5θcos3θdθ

the solution to this would be:

this follows from: sin(A+B) +sin(A-B) = 2sinAcosB

$$sinAcosB =\frac{1}{2}[sin(A+B)+sin(A-B)]$$

in our case: A=5θ and B = 3θ

hence:

$$sin5θcos3θ = \frac{1}{2}[sin(5θ+3θ)+sin(5θ-3θ)]$$

$$=\frac{1}{2}[sin8θ+sin2θ]=\frac{1}{2}sin8θ+\frac{1}{2}sin2θ$$

therefore:

$$\int sin5θcos3θdθ = \frac{1}{2} \int (sin8θ+sin2θ)dθ$$

$$\int sin8θ = \frac{1}{8}cos8θ \ \ \ \ and \int sin2θ=\frac{1}{2}cos2θ$$

it follows that:

$$\frac{1}{2}\int(sin8θ+sin2θ)dθ =\frac{1}{16}cos8θ+\frac{1}{4}cos2θ+c$$

Example 2

work out: ∫sin3θcos²θdθ

you can proceed as follow:

from double angle identities:

$$cos^2θ = \frac{1+cos2θ}{2}dθ$$

therefore

$$sin3θ(\frac{1+cos2θ}{2})dθ = \frac{1}{2}\int sin3θ+\frac{1}{2} \int sin3θcos2θ$$

but

$$sin3θcos2θ = \frac{1}{2}(sin5θ+sinθ)$$

$$\frac{1}{2} \int sin3θ +\frac{1}{2}\int sin3θcos2θ$$$$=\frac{1}{2} \int sin3θdθ+\frac{1}{2} \int \frac{1}{2}(sin5θ+sinθ)dθ$$

$$\frac{1}{2}\int sin3θdθ+\frac{1}{4} \int sin5θdθ+\frac{1}{4} \int sinθdθ$$

$$-\frac{1}{6}cos3\theta-\frac{1}{20}cos5θ-\frac{1}{4}cosθ+c$$

Integration of trigonometric expressions

some know trigonometric functions and identities

2. Using trigonometric identities

3. Substitution Method

Integration of trigonometric expressions: 4. Integration by Parts

Integration of trigonometric expressions: Trigonometric Substitution

Integrating Even powers of sine and cosine

Example problem on trigonometric substitution

Example2

Solving Integrating trigonometric expressions with odd powers

Integration of trigonometric expressions: Multiple angles identities

Example 6

Related Topics

More posts

Gradient of a line

Basic Electronics Exam Questions

The Intrinsic and extrinsic semiconductors

High school Physics Exam papers