Fundamental theorem of calculus

The Fundamental Theorem of Calculus  establishes a crucial link between differentiation and integration.

 It essentially states that these two operations are inverses of each other, and it provides a way to evaluate definite integrals using anti-derivatives.

Suppose that f is continuous at a closed interval [a, b] . If the function F is defined on a closed interval [a, b] by:

where a is a real number, Then F is the anti-derivative of f. in other words, F'(x) = f(x)

consider the relationships:

then

f(x) = x² and

Note: We use the dummy variable (t) in the integrand to avoid confusion with the upper limit x.

Sometimes the fundamental theorem of calculus is interpreted to mean that:

differentiation and integration are inverse processes to each other.

It follows that:

The fundamental theorem of calculus states that:

if f is continous on an open interval containing a and x and then we first integrate the function f and then differentiate with respect to x, then the result we get is the function f again.

In other words, the fundamental theorem of calculus argues that differentiation cancels the effect of intergration of continous f(x’).

in short:

For example

Example problem1

Use the fundamental theorem of calculus to find derivative of the following functions

(a)

solution

NOTE: The best way to benefit from this examples is trying the problem first before looking for answers and attempting again after checking your work against the answer.

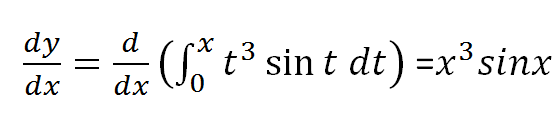
Example problem2

(b)

solution to problem 2

Example problem 3

Find h'(x) given that :

solution

let y=h(x) and u=x² and hence:

since u=x²;

and therefore:

By use of chain rule:

which implies u³sinu(2x) = (x²)³sin(x²)2x resulting to:

=2x⁷sin(x²)

Example problem 4

Consider the expression below, we exchange the limits in the intergral and then change the sign from positive to negative before using the fundamental theorem to solve it.

Example problems on fundamental theorem of calculus

We exchange limits and so the sign of the integral so that the upper limit is the valuable x.

Example problem 6

Use the fundamental theorem of calculus to solve:

Solution

splitting the integral about point zero we have:

and then exchanging limits in the first integral;

let u=-x; first part of the expression above becomes;

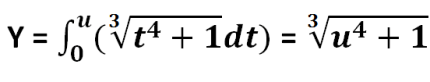
from laws of differentiation du/dx=-1 and using chain rule;

and hence

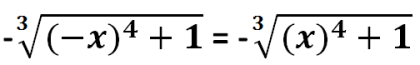
and finally

Revision Exercise

Answers to revision exercise

Related topics

• Basic Integration rules
• The second fundamental theorem of calculus

---