The decay law is an exponential decay law that describes the spontaneous transformation of unstable atomic nuclei into more stable ones by emitting radiation.
The decay law states that the rate of disintegration at a give time is directly proportional to the number of nuclides present at that time.
Radioactive decay is described as a spontaneous, random process in which the nuclide that will disintegrate next cannot be predicted. Time and chances determines the next nuclide to decay.
let N be the number of nuclides present at the current time.
then rate of change of N (dN) in respect to change of time(dt) is directly proportional to the existing number of nuclides available. That is:
Introducing a constant of the above proportionality which is known as the decay constant we get: λ
The negative sign in the equation above indicates that the number of nuclides N decreases with increase of time.
Half-life in radioactivity
Half life is the time taken for half of nuclides present in a radioactive sample to decay to half of their total number. For example if there 10000 nuclides in a sample, the time taken for them to reduce to 5000 due to radioactivity is the half life of the involved element.
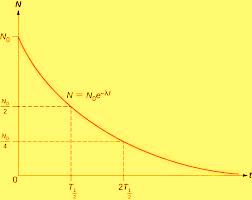
It can be shown that the number of nuclides remaining undecayed , N, after a period of time T will be given by:
The number of nuclides that remains after every half life can be plotted against a number of half lives to have the shape shown:

Example problems of decay law
The half life of a certain radioactive element is 16 years. What fraction of the element with have decayed after: (a) 48 years, (b) 80 years
solution
The amount remaining after T years will be given by:
for 48 years:
(b)